Die Energieeinsparung bei der Heizung durch den Einsatz von Thermokeramikmembranen.

Abschlussbericht über die Ergebnisse des Projekts Transfer Bonus

Verbesserung des Innenklimas und Energieeinsparung für die Heizung durch die Technologie der thermokeramischen Membranen (ClimateCoating) als Innen- und/oder Außenbeschichtung von Gebäuden.

Erstellt von:

• INBITEC e.V., Institut für biologisch-medizinische Forschung und Technologie e.V. (Institut für biologisch-medizinische Forschung und Technologie, Berlin)
• Senatsverwaltung für Wirtschaft, Technologie und Forschung (Senat für Wirtschaft, Technologie und Forschung), Berlin
• COMSOL Certified Consultants

Mit der Berechnungsmethode der Finite-Elemente-Methode ist es erstmals möglich, komplexe physikalische Prozesse und Abläufe mit allen beteiligten physikalischen Prozessen sichtbar zu machen. Auf diese Weise können verschiedene Einflüsse und Quellen visuell und anschaulich dargestellt werden, die ursprünglich unabhängig auf das Gesamtsystem wirken. Ziel der Untersuchung ist es, Informationen darüber zu liefern, wie der Wärmeeffekt im Detail abläuft und welche Parameter zur Optimierung beeinflusst werden können.

Einleitung

Die Farbe ClimateCoating mit einer Zusammensetzung von 50 % keramischen Vakuumhohlkugeln im Bereich µm und einem Bindemittel auf Acrylatbasis für die Innen- und Außenbeschichtung zeigt eine hohe Stabilität sowie eine Reihe von vorteilhaften Eigenschaften für die Wärmeisolierung und die Verbesserung des Innenklimas. Durch das Verständnis der einzelnen physikalischen Prozesse können Rückschlüsse auf den Effekt gezogen werden. Darüber hinaus sollten Animationen des zeitlichen Ablaufs während des Heizens mit verschiedenen Heizquellen detaillierte Erkenntnisse für den Entwickler sowie eine visuelle Erklärung des Heizeffekts für den Verbraucher liefern.

Simulationen (Finite-Elemente-Methode-FEM) des Innenklimas (Temperaturverteilung, Luftströmung, Konvektion, Wärmestrahlung, Wärmeleitung) (AP 1)

Rechnbarer Schritt: Entwurf eines identischen zweidimensionalen Modells gemäß den Spezifikationen zur Verbesserung des Innenklimas mit Animation (rechnbarer Schritt für die 3. Projektwoche)

Um Klimamodelle im Raum zu testen, wurden zunächst die erforderlichen physikalischen Prozesse im Raum-Modell mit Varianten des Raumklimas dargestellt. Zu diesem Zweck wurde der Heizfall für die Wintersituation und der Kühlfall für die Sommersituation programmiert und getestet:

Heizschrank für das Deckenheizungssystem

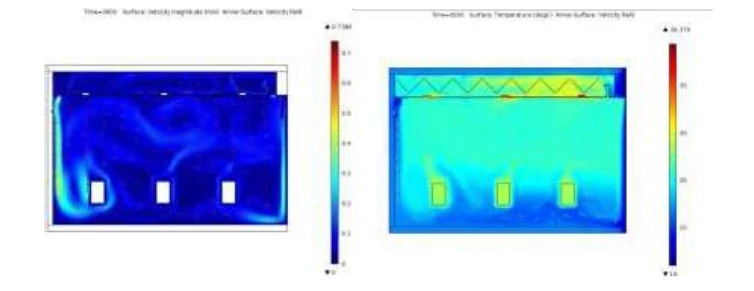
Abb. 1 Verlauf der Luftströmung links und Temperaturverteilung rechts im Büroraum mit Strahlungsheizung an der Decke und konstantem Lüften. Kälte dringt durch das Fenster an der rechten Fassade ein. Drei Rechtecke in der Mitte des Raumes simulieren die Wärmebelastung durch Geräte oder Personen.

Kühlschrank für das Deckenklimasystem

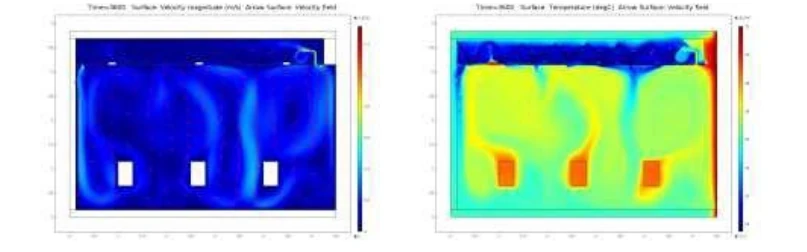
Abb. 2 Verlauf der Luftströmung links und Temperaturverteilung rechts im Büroraum, klimatisiert durch Kühlmatten an der Decke und kontinuierliche Belüftung. Die Wärme dringt durch das Fenster an der rechten Fassade ein. Drei Rechtecke in der Mitte des Raumes simulieren die Wärmebelastung durch Geräte oder Personen.

Fazit: Die Klimasimulationen, die zur Prüfung der Modelle des Innenklimas entwickelt wurden, konnten alle physikalischen Prozesse darstellen. Die hohe Transparenz ermöglichte eine detaillierte Untersuchung aller einzelnen Prozesse.

Simulationen der Verbesserung des Innenklimas durch keramische Hohlkugeln in der Farbbeschichtung (ClimateCoating) und Interpretation des einfachen Jalousieneffekts der Hohlkugeln (AP2)

Rechnbarer Schritt: Entwurf eines identischen dreidimensionalen Modells gemäß den Spezifikationen zur Verbesserung des Innenklimas mit ClimateCoating-Farben mit Animation. (Diskussion und Präsentation der ersten Ergebnisse). Abrechenbarer Schritt für die 4. Projektwoche.

Zur Untersuchung der Prozesse in der ClimateCoating-Beschichtung war es notwendig, ein nahezu identisches Mikromodell zu entwickeln, das die Anordnung der Hohlkugeln mit statistischer Verteilung von Position und Größe reproduziert. Zu diesem Zweck wurde eine mathematische Methode für die statistisch verteilte Anordnung dieser Kugeln in einem Würfel mit den Abmessungen 300 x 500 x 500 entwickelt, die sowohl im optischen Programm (OptiCAD) als auch im Finite-Elemente-Programm (Comsol Multiphysics) implementiert werden konnte.

Anordnung der Kugeln für die Testberechnungen

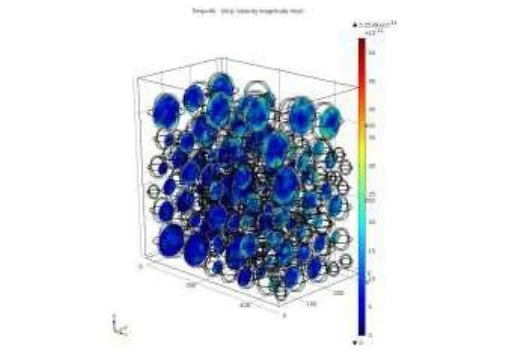
Abb.3 Statistisch verteilte und größenvariable Anordnung der Kugeln in einem kubischen Volumenkörper

Anschließend wurden Studien zur Lichtstreuung auf einer Hohlkugel sowie auf diesem Testwürfel durchgeführt.

In der frequenzabhängigen Studie zwischen 10 und 22 THz oder 13 und 30 µm wurden die folgenden Strahlungsprofile für die Intensität des elektrischen Feldes ermittelt, wenn das Strahlungsfeld auf die Hohlkugel traf.

Strahlungsprofile auf der Hohlkugel

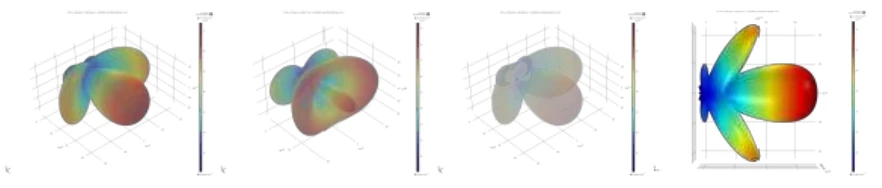
Abb.4 Strahlungsprofile des elektrischen Feldes, wenn eine ebene Welle auf die Hohlkugel bei verschiedenen Wellenlängen trifft.

Die Abbildungen zeigen Beispiele für einige einzelne räumliche Profile.

Diese Studie zeigt eindeutig nahezu direkte Strahlungsintensitäten, die einen vernachlässigbaren Rückstreuungsanteil bilden.

Mit derselben Anordnung der Kugeln wurde auch eine Strahlanalyse im optischen Programm durchgeführt (Strahlverfolgung). Auch hier wurde der parallele Strahl auf den Würfel mit den Kugeln gerichtet (siehe Abb. 3). Es ist zu sehen, dass wieder eine direkte Streuung auftritt (Abb. 5), die nur an der Wand reflektiert wird. Erst wenn den Kugeln auf der Oberfläche eine vollständige Reflexion zugewiesen wird (Abb. 6), erfolgt die Rückstreuung. Diese Rückstreuung bleibt jedoch fast vollständig in der Farbschicht wie in einem Lichtleiter, wie in Abb. 7 zu sehen ist.

Strahlverfolgung auf einem Würfel, der mit SiO2-Hohlkugeln gefüllt ist

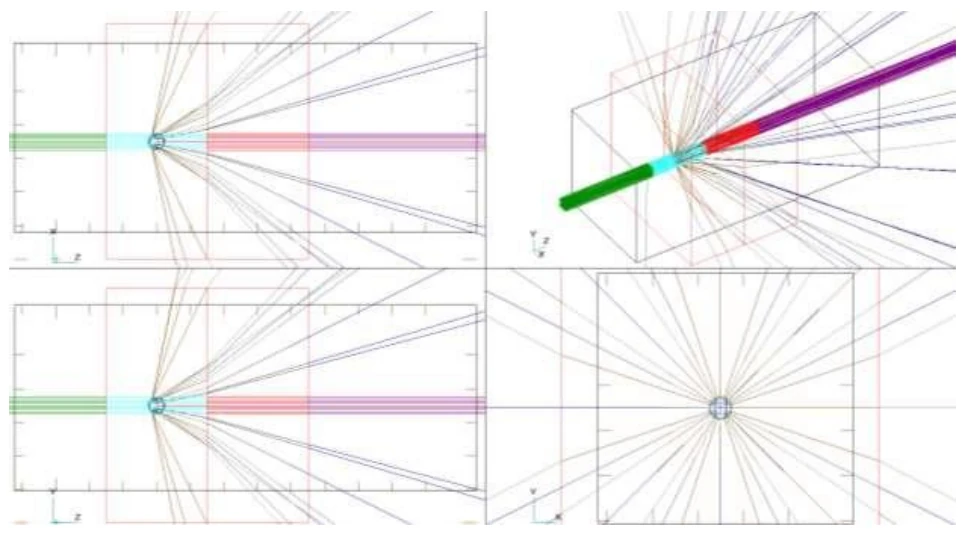
Abb.5 Das Modell stellt eine SiO2-Hohlkugel dar, die in eine Acrylschicht eingefügt ist. Dahinter befindet sich eine _{Betonwand, für die zur besseren Erkennbarkeit keine hohe Absorption zugewiesen wurde.} Das Ergebnis ist eine Strahlung, die ausschließlich nach vorne gerichtet ist und dann absorbiert wird. Dies führt zum Erwärmen der Farbschicht.

Strahlverfolgung auf einem Würfel, der mit spiegelnden SiO2-Hohlkugeln gefüllt ist

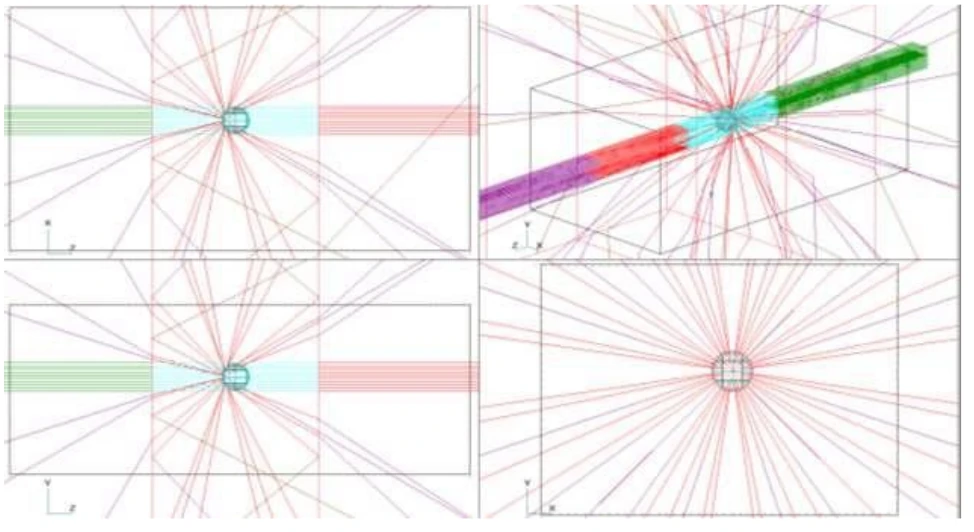
Abb.6 Das Modell ist identisch mit dem Modell in Abb. 5, jedoch hat die Kugel hier einen Reflexionsfaktor von Eins. Auch hier bleiben fast alle Strahlen in der Acrylfarbe, und sie tauchen nicht mehr auf. Dies führt wiederum zum Erwärmen der Farbschicht.

Strahlverfolgung auf einem Würfel, der mit SiO2-Hohlkugeln gefüllt ist, mit einer erweiterten Farbschicht

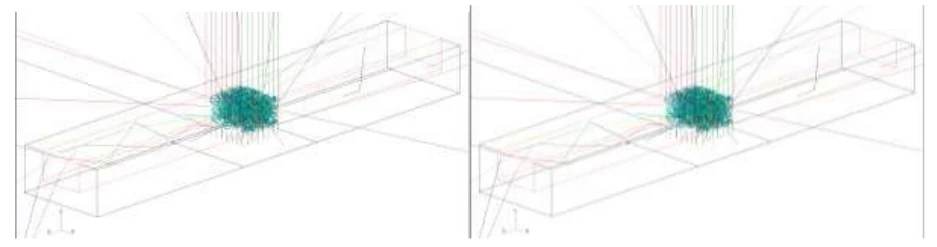
Abb. 7 Das Modell der Kugel ist identisch mit dem in Abb. 5. Die Kugeln haben links die natürliche Oberfläche und rechts einen Reflexionsfaktor von Eins. In beiden Fällen ist das Bild ähnlich: Alle Strahlen bleiben in der Acrylfarbe, die hier verlängert wurde, und tauchen nicht mehr auf. Dies führt in beiden Fällen zu einer Erwärmung der Farbschicht.

Strahlverfolgung auf einem Würfel, der mit SiO2-Hohlkugeln gefüllt ist, mit einer erweiterten Farbschicht

Abb. 8 Zwei Streudiagramme wurden auf einem flächigen Detektor aufgenommen, der als Rechteck unter dem Kugelwürfel in Abb. 7 erkennbar ist. Im linken Fall mit natürlichen Kugeln beträgt die Rückstreuung etwa 10 % der bestrahlten Strahlen, im rechten Fall beträgt die Rückstreuung etwa 35 %.

Fazit: In diesem Schritt wurde die Streuung und Reflexion im Mikrorraum in dreidimensionalen Modellen untersucht. Es wurde eindeutig gezeigt, dass eine wichtige Eigenschaft der Farbe ihre Streuung und Absorption in einer dünnen Farbschicht ist. Im Gegensatz zur vorherigen Annahme ist jedoch die Reflexivität gering. Im Rahmen der Optimierung muss der Einfluss der diskutierten Oberflächenbeschichtung mit einer metallischen Reflexionsschicht (z. B. Aluminium) in weiteren Entwicklungsprojekten untersucht werden. Dies erfordert jedoch auch spezielle metrologische Untersuchungen als Datenlieferanten für die Simulation.

Interpretation der bestehenden Messergebnisse mittels Simulationen unter Berücksichtigung der Ergebnisse aus Pankow, München und der Pergula-Gruppe (WP 3)

Pflichtschritt: Interpretation der bestehenden Messergebnisse durch Simulationen unter Berücksichtigung der Ergebnisse aus Pankow, München und der Pergula-Gruppe. (Abrechenbarer Schritt für die 7. Projektwoche)

Für die Simulation des Pankow-Experiments wurden drei Modelle berechnet:

1. Eine halbe Töpferform mit einem ungeglasten Tonbehälter und einer Wärmequelle in der linken Ecke der rotierend symmetrisch berechneten Scheibe.
2. Eine halbe Töpferform mit einem im Inneren mit Acryl beschichteten Tonbehälter und einer Wärmequelle in der linken Ecke der rotierend symmetrisch berechneten Scheibe.
3. Eine halbe Töpferform mit einem im Inneren mit Acryl beschichteten Tonbehälter und Hohlmikrokugeln von etwa 50 % und einer Wärmequelle in der linken Ecke der rotierend symmetrisch berechneten Scheibe.

Messpunkte für die folgenden Diagramme mit entsprechender Nummerierung

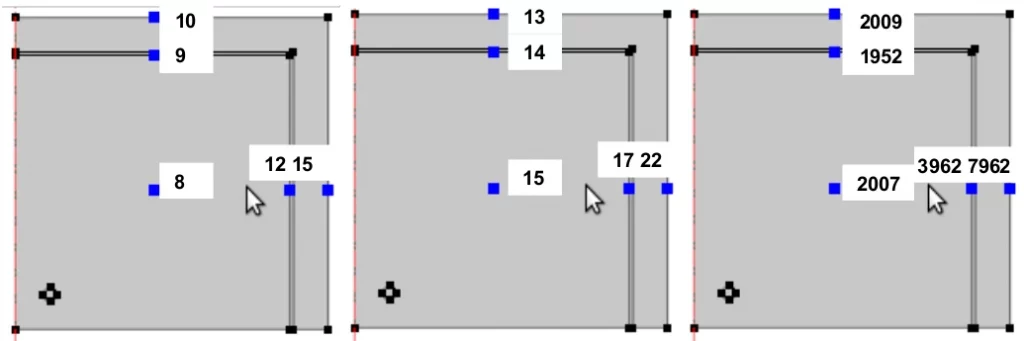
Abb. 9 Zur Berechnung des Pankow-Experiments wurden drei räumliche Scheiben modelliert, die mit der Symmetriebedingung einer rotierend symmetrischen Anordnung eine Geometrie ähnlich einem Blumentopf führten. Für die Bestimmung der Erwärmung wurden Messpunkte definiert, um ein Diagramm zu erstellen, das ihre Positionen anzeigt, die in dieser Darstellung nummeriert sind.

Mit den in Abb. 9 dargestellten Modellen wurden die Bedingungen des Blumentopfs-Experiments wiederhergestellt. Der obere und rechte Rand wurde dem Ton Material zugeordnet, die folgende dünne Schicht war in jedem Fall ohne Farbe (a), in der Mitte mit Acrylfarbe (b) und rechts mit Imoshfarbe (c), aber regelmäßige Hohlkugeln wurden verschoben. Das Innere wurde als Luft programmiert. Links unten wurde eine Wärmequelle mit 15 W Leistung eingefügt. Die berechnete Erwärmungszeit betrug 6 Minuten.

Temperaturprofile nach 5 Minuten Erwärmung

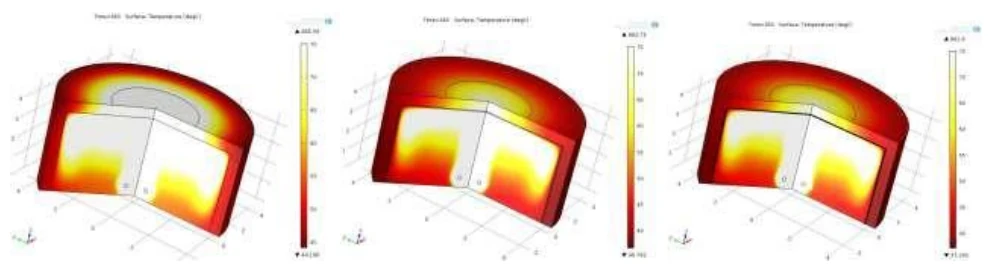
Abb.10 Berechnungsergebnisse der Temperaturverteilung bei Erwärmung mit einer Wärmequelle von 15 W. Die Bilder zeigen, dass im Fall (a) eine deutlich höhere Erwärmung des oberen Teils des Blumentopfs auftritt, die in den Fällen (b) und (c) reduziert wird. Die Temperaturerhöhung ist in den folgenden Diagrammen deutlicher zu erkennen.

Mit den Messpunkten, die in Abb. 9 dargestellt sind, konnten nun die Temperaturkurven grafisch bestimmt werden. Analog zum Pankow-Experiment zeigte Fall c) einen Temperaturanstieg und eine vorteilhafte Temperaturverteilung.

Fazit: In diesem Arbeitsschritt wurde das Verhalten der Streuung und Reflexion mit Mikrokugeln in 3D-Modellen untersucht. Eine nahezu gleichmäßige Temperaturverteilung im Inneren, die für den menschlichen Komfort vorteilhaft ist, kann nur mit Mikrokugeln im Acrylat erreicht werden.

In den drei simulierten Testserien, ebenso wie im Pankow-Experiment, zeigt nur das Diagramm rechts einen deutlichen Temperaturanstieg im Vergleich zu den beiden Diagrammen links. Der Unterschied in der Temperatur zwischen den inneren und äußeren Wänden ist ebenfalls etwas größer. In dieser Simulation wurden also sehr ähnliche Ergebnisse erzielt.

Temperaturprofile nach 5 Minuten Erwärmung

Abb. 11 Berechnungsergebnisse der Temperaturen an den Messpunkten in den drei oben beschriebenen Fällen bei Erwärmung mit einer Wärmequelle von 15 W. Aus den Diagrammen ist ersichtlich, dass die inneren Temperaturen im Laufe von 6 Minuten von links nach rechts ansteigen und auch die Erwärmung der äußeren Messpunkte von links nach rechts verringert wird.

Zusätzlich zu den dynamischen Berechnungen über 6 Minuten wurde für alle drei Fälle auch eine statische Berechnung durchgeführt, um den Endzustand zu ermitteln.

Statische Berechnung der Erwärmung des „Blumentopfs“

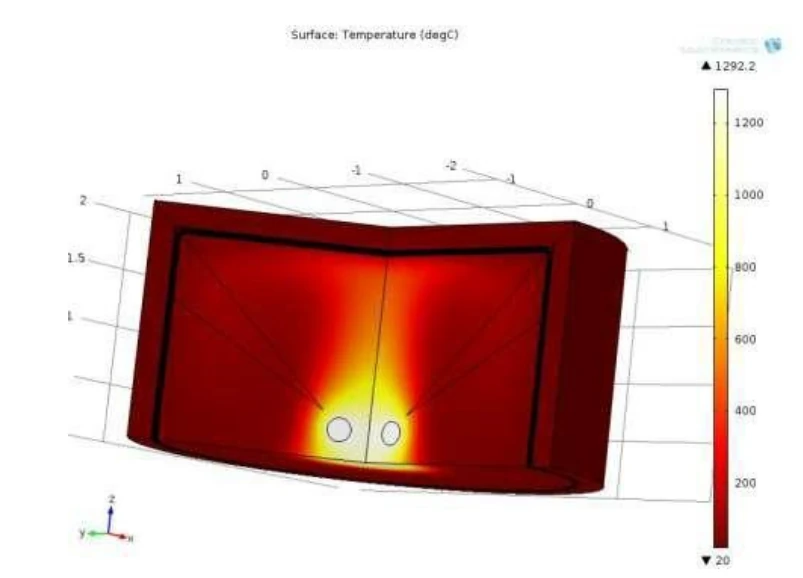
Abb. 12 Repräsentatives Ergebnis der statischen Berechnung der Temperaturen mit Darstellung der diagonalen Linien, entlang denen die Endtemperatur für alle drei Fälle ermittelt wurde.

Das Ergebnis dieser Berechnungen war auch die Bestimmung der Temperaturunterschiede, die im Experiment für diese drei Fälle festgelegt wurden:

Statische Berechnung der Erwärmung des „Blumentopfs“

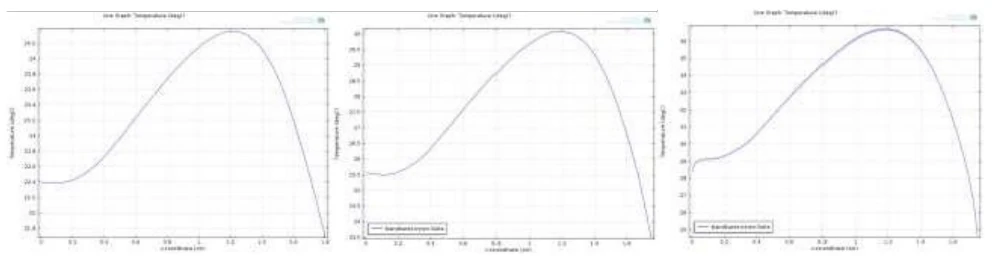
Abb. 13 Endtemperaturen entlang der Diagonale, die auf Abb. 12 für die drei Beschichtungsfälle in der statischen Berechnung gezeichnet wurde. Laut den Ergebnissen des Pankow-Experiments zeigt es auch einen „gleichmäßigen“ Temperaturanstieg von links nach rechts. Es ist zu beachten, dass die Skalierung für die Fälle a), b) und c) unterschiedlich ist. Im Fall c) ist die Kurve aufgrund der Mikrokugeln leicht überkreuzt.

Die Berechnungen wurden durchgeführt, um die Finite-Elemente-Methode anhand experimenteller Daten zu überprüfen. Vergleichbare Ergebnisse wurden bereits in diesem Experiment erzielt, das auch von uns wiederholt wurde, sodass dieser Ansatz bestätigt wurde. Ein ähnlicher Ansatz wurde auch im Münchener Experiment angewendet. Dieses Modell wurde vollständig reproduziert und in drei Dimensionen berechnet. Solch eine Berechnung ist aufgrund der sehr hohen Anzahl an Finite-Elementen zeitaufwändig und wurde daher nur für Porenbetonwände (Münchener Experiment) durchgeführt. Die gleiche experimentelle Anordnung mit Holzwänden (Pergula-Experiment) ändert nur die physikalischen Werte des Wandmaterials. Daher war es für die Programmierung nicht mehr nützlich und wurde daher nicht durchgeführt.

Berechnung der Erwärmung des isolierten Würfels Münchener Experiment

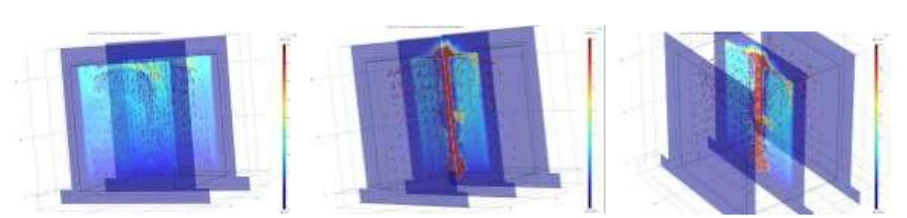
Abb. 14 Berechnung des Erwärmungsexperiments im Inneren des Würfels mit einer Wärmequelle von 15 W und Wänden aus Porenbeton (a), zusätzlich mit Acrylbeschichtung (b) und mit ClimateCoating-Beschichtung (c). Ähnlich wie im Fall des Blumentopfs wurde die Temperatur im Inneren besonders im Fall c) erhöht.

Temperaturkurven im simulierten Münchener Experiment

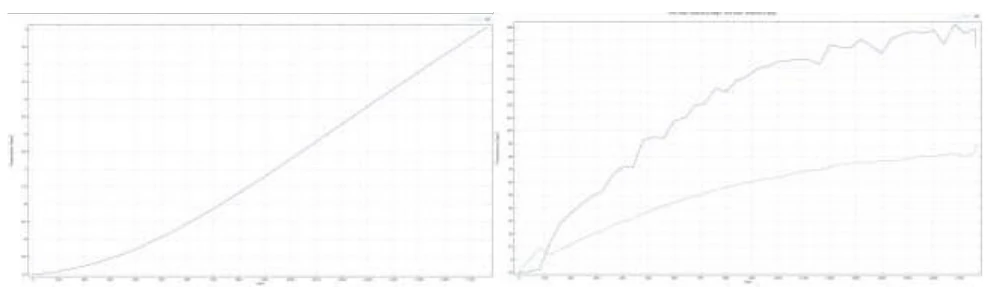
Abb. 15 Berechnung des Erwärmungsexperiments im Inneren des Würfels mit einer Wärmequelle von 15 W und Wänden aus Porenbeton (a), zusätzlich mit Acrylbeschichtung (b) und mit ClimateCoating-Beschichtung (c). Ähnlich wie im Fall des Blumentopfs wurde die Temperatur im Inneren besonders im Fall c) erhöht.

Fazit: Beide Experimente konnten simuliert werden und lieferten konsistente Ergebnisse für den Temperaturanstieg. Dies bewies, dass die Finite-Elemente-Methode, die mit dem Comsol Multiphysics-Programm verwendet wurde, eine gültige m-Methode zur Simulation realer Wärmeprozesse ist.

Berechnungsmodul zur Optimierung der Verteilung des Durchmessers keramischer Hohlkugeln (WP 4)

Abrechenbarer Schritt: Berechnungen zur Verbesserung der Rückstreuungseigenschaften durch die hinzugefügten keramischen Kugeln in den Farben und computergestützte Berechnungen zur Anpassung der Farben an Infrarotstrahler (Diskussion und Präsentation der Ergebnisse) (abrechenbarer Schritt für die 10. Projektwoche)

Nachdem zunächst die Eigenschaften der Mischung von Hohlkugeln in ihren Infrarot-Optikeigenschaften bestimmt wurden, speziell mit dem Prozess der Absorption des größten Teils der einfallenden Strahlung, wurde nun der nächste Teil der Farbeigenschaften untersucht. Bei der simulierten Methode im Querschnittsraum wurde die Farbschicht in zwei Teile unterteilt und gemäß der Beimischung von 50 % Vakuumkugeln wurde eine Hälfte der Farbschicht (0,025 mm) als vakuumiert und die andere Hälfte (ebenfalls 0,025 mm) als Acrylfarbe programmiert. Diese wurde auf die linke Seite des Modells aufgetragen und auf die rechte Seite wurde eine 0,3 mm dicke Schicht reines Acryl aufgetragen. Der Querschnittsraum wurde für eine Stunde bei einer Temperatur von 30 °C mit einer Wärmestrahlungsquelle beheizt, beginnend bei 10 °C für alle Komponenten. Der Erwärmungsprozess während der einstündigen Heizphase wurde auf einer „Personenfigur“, die in den Raum gestellt wurde, berechnet, wobei die Temperatur 37 °C betrug und eine Wärmeleistung von 80 W ausgegeben wurde. Die „Personenfigur“ wurde dann auf eine Temperatur von 30 °C erwärmt. Die „Personenfigur“ wurde dann auf eine Temperatur von 37 °C erwärmt. An der „Personenfigur“ wurden an markierten Stellen Messpunkte angebracht, deren Temperaturkurven dann in einem Diagramm ausgewertet werden konnten.

Um auch die Reflexionseigenschaften der Farbe zu bestimmen, wurden drei Tests mit unterschiedlichen Reflexionseigenschaften für beide Farbschichten durchgeführt.

Da die Beschichtung auch bei strukturellen Kältebrücken in früheren Anwendungen positive Eigenschaften gezeigt hat, wurde auch eine künstliche Kältebrücke über dem Boden verwendet, die mit einer Außentemperatur von -10 °C bedeckt war. Gleichzeitig wurde die Strömungsgeschwindigkeit berechnet, um weitere Erkenntnisse zu gewinnen. Gleichzeitig wurde die Luftströmung in den Berechnungen bestimmt, um weitere Erkenntnisse zu gewinnen.

Geometrie für die Testläufe

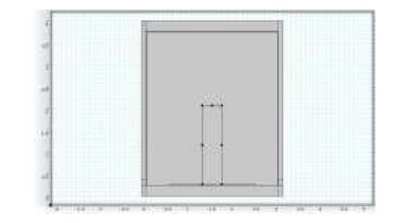
Abb. 16 Darstellung der Geometrie, die bei den drei Tests und Messpunkten des getesteten Objekts verwendet wurde.

Temperaturprofile der Erwärmung des Querschnittsraums nach einer Stunde Heizen

Abb. 17 Darstellung der Endtemperaturprofile nach einer Stunde Erwärmung für die drei Fälle der erneuten Erwärmung von Farbschichten. Auf der linken Seite wurde ClimateCoating-Farbe simuliert und auf der rechten Seite Standard-Acrylfarbe. Eine Hälfte der linken Farbschicht bestand aus einer Vakuumschicht mit einem Druck von 1/100 des Normaldrucks und die andere Hälfte aus Acrylfarbe. In allen drei Fällen war die Erwärmung auf der linken Seite eindeutig besser.

Strömungsprofile der Erwärmung des Querschnittsraums nach einer Stunde Heizen

Abb. 18 Darstellung der Endströmungsprofile nach einer Stunde Erwärmung für die drei Fälle der Reflexion von Farbschichten. Auf der linken Seite wurde ClimateCoating-Farbe simuliert und auf der rechten Seite Standard-Acrylfarbe. Die Hälfte der Farbschicht auf der linken Seite bestand aus einer Vakuumschicht mit einem Druck von 1/100 des Normaldrucks und die andere Hälfte aus Acrylfarbe. In allen drei Fällen war die Luftturbulenz auf der linken Seite aufgrund der schnelleren Erwärmung deutlich höher.

Temperaturkurve basierend auf diesen dynamischen Berechnungen zeigt die erwarteten Temperaturunterschiede in der Mitte und an den Füßen der getesteten Person. An der Kopfseite sind die Temperaturen nahezu gleich, da sie durch die Luftzirkulation ausgeglichen werden (siehe Abb. 16).

Körpertemperatur des getesteten Subjekts

Abb. 19 Darstellung der Temperaturkurven des Testsubjekts in den drei untersuchten Fällen unterschiedlicher Reflexion der Farbe. Sie zeigen deutlich eine stärkere Erwärmung auf der linken Seite während der Erwärmungsphase.

Fazit: Ein Teil der Gründe für die Verbesserung des Raumklimas konnte bereits in dieser Studie nachgewiesen werden. Dies beruht auf der schnelleren Erwärmung der dünnen Acrylschicht aufgrund der Wärmeschirmung durch die Vakuumschicht. Die deutliche Erwärmung der linken Seite wird durch die zusammenhängende Vakuumschicht verursacht, die in diesen Untersuchungen verwendet wurde. Sie liefert jedoch das gewünschte Ergebnis der möglichen Optimierung: Da die Vakuumisolierung eine so deutliche Verbesserung bringt, kann die Erweiterung der Vakuumkugeln auf den Bereich der Streuung von 50 – 250 µm sicherlich eine klare Optimierung der Farbe bringen. Diese Vergrößerung führt zu einer deutlichen Erhöhung des Volumens des Vakuums, ähnlich wie im Fall der hier simulierten zusammenhängenden Schicht. Die Erhöhung der Reflexivität der Farbe ClimateCoating von einem Reflexionsfaktor von 0,5 auf 1,0 führte ebenfalls zu einer leichten Erhöhung der Temperatur, sodass in Zukunft auch Experimente in dieser Hinsicht durchgeführt werden sollten. Die Berechnungen haben also auch in diesem Fall eine wichtige Optimierungsbehauptung geliefert!

Berechnungen zur Verbesserung der Rückstreuungseigenschaften (Mie-Streuung und Rückstreuung im Infrarotbereich) durch Zugabe von Keramikkugeln zu Farben und computergestützte Berechnungen zur Anpassung der Farben an Infrarotstrahler. (WP 5)

Abrechenbarer Schritt: Simulationen der Energieeinsparung durch Heizung durch die Verwendung der Technologie von Thermokeramikmembranen für Innen- und/oder Außenanstriche von Gebäuden (Diskussion, Präsentation und Animation der ersten Ergebnisse). Woche 12

Infrarotstrahlung und Streuung können durch diese physikalischen Phänomene beschrieben werden:

1. Makroskopische deterministische Phänomene:
   • Auf dem Übertragungsweg von IR-Strahlung kann die Energie der Strahlung in drei Komponenten unterteilt werden: „Reflexion“, „Absorption“ und „Übertragung“. Reflexion, Übertragung sowie Brechung und Beugung sind Interferenzphänomene, die mit der Mie-Streuung beschrieben werden können (siehe Punkt 2). Absorption gehört jedoch zur Kategorie 3.
2. Mikroskopische deterministische Phänomene
   • Mie-Streuung kann durch Interferenz sekundärer Wellen beschrieben werden, die durch die primäre Welle an den Grenzflächen zwischen Materialien mit unterschiedlichen elektromagnetischen Eigenschaften angeregt werden (Huygens’sches Prinzip).
   • Phasenübergangsphänomene können den Unterschieden in den Feldkonstanten der verwendeten Materialien zugeschrieben werden. In diesem Fall sind alle Materialien elektrisch nicht leitend und nicht magnetisch. Daher ist die Permittivität (Dielektrizität) der einzige Materialparameter, der die Mie-Streuung verursacht.
3. Makroskopisch-statistische Phänomene
   • Emission durch den Strahler (in diesem Fall sind nur „Strahler mit Planck-Temperatur relevant“). Für den Einsatzbereich von ClimateCoating-Beschichtungen wurde ein Temperaturbereich von -40 °C bis 120 °C angenommen. Die spektrale Leistung oder Energiedichte über 50 % des Maximums liegt im Wellenlängenbereich von etwa 4 bis 24 µm. Diese Wellenlängen fallen in den Bereich der Abmessungen von Glas-Keramikkugeln. Daher wird angenommen, dass Mie-Streuung ein relevantes Phänomen ist, das zunächst gerechtfertigt ist.
   • Absorption erhöht die Temperatur des absorbierenden Materials durch Anregung der inneren Bewegung (räumliche Oszillationen von Atomen/Molekülen). Absorption als Materialeigenschaft kann durch den imaginären Teil der komplexen Permittivität ausgedrückt werden.
4. Mikroskopisch-statistische Phänomene
   • Im betrachteten Bereich ist jedoch die Permittivität stark von der Wellenlänge oder Frequenz abhängig. Diese Abhängigkeit beruht insbesondere auf atomaren und ionischen Resonanzen sowie auf orientierender Polarisation. Die Effekte hängen stark von der molekularen Zusammensetzung und Struktur der Materialien ab. Elementare Wechselwirkungen im Infrarotbereich können durch quantenmechanische Wechselwirkungen zwischen Photonen und optischen Phononen erklärt werden. Diese Daten können aufgrund unzureichender Daten nicht berechnet werden.

Die stärksten elektromagnetischen Effekte der Grenzflächen treten in der ClimateCoating-Beschichtung zwischen der Hohlkammer und den Glas-Keramikkugeln auf. Zwischen der Glas-Keramik und der Acrylmatrix gibt es nur geringe Unterschiede in der Permittivität abgesehen von der Frequenzabhängigkeit. Der Einfluss dieser Grenzflächen könnte daher vernachlässigt werden.

Um die Mie-Streuung unabhängig von den strukturellen Umwelteinflüssen zu simulieren, wurde eine Simulation für eine sphärische Hohlkammer (Vakuum) im unendlich ausgedehnten Siliciumoxid durchgeführt.

Dieses Modell ermöglicht

1. Exakte quantitative Darstellung der Richtungsabhängigkeit der Mie-Streuung als Funktion des Wellenlängen-/Objektgrößenverhältnisses.

1. Maximale Darstellung der richtungsabhängigen Maxima und Minima der Streuung
2. Gute Abschätzung des extremen Wertes des Streueffekts

Für die primäre Strahlung wurde eine monofrequente ebene Welle mit unendlicher Kohärenzlänge angenommen, die bei Auftreffen auf die Materialgrenze interferierende sekundäre Wellen anregt.

Bei der Darstellung des Streueffekts wurde nur das angeregte sekundäre Strahlen berücksichtigt, da in der Praxis auch dieses mit der primären Strahlung interferiert und die Streuungseigenschaften daher nur näherungsweise erstellt oder überhaupt nicht unterschieden werden können.

Da die Streueigenschaften nicht von der absoluten Wellenlänge und der Größe des Objekts abhängen, sondern von deren Verhältnis, wurde für die Simulation ein Durchmesser der Referenzkugel von 20 µm gewählt. Das bedeutet, dass die Ergebnisse für andere Durchmesser durch einfache Kalibrierung der Wellenlänge übertragen werden können.

Um nur die Abhängigkeiten der geometrischen Beziehungen zu analysieren, wurde die Simulation mit einer frequenzunabhängigen Permittivität durchgeführt.

In den Streudiagrammen wurde eine starke Abhängigkeit von der Wellenlänge und sehr ausgeprägte richtungsabhängige Maxima und Minima festgestellt. Es war auch ein Rückgang der Richtwirkung in Richtung der Grenzwerte des entsprechenden Infrarotbereichs deutlich zu sehen.

Streumuster auf einer Hohlkugel

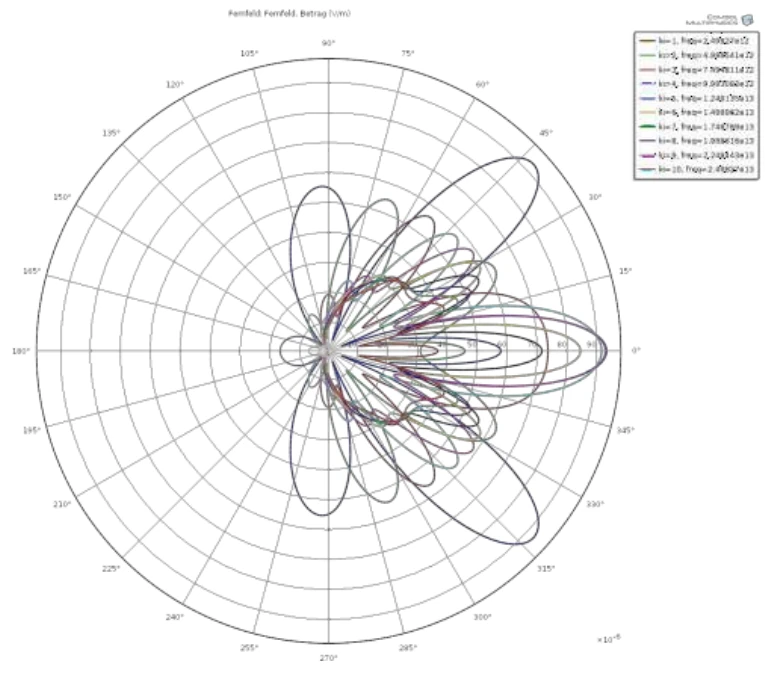
Abbildung 20: 2D-Streumuster für das entfernte elektrische Feld, wenn eine ebene Welle auf eine Hohlkugel mit unterschiedlichen Wellenlängen trifft.

Die größten Maxima der Streuung treten in Richtung der Bestrahlung (von links nach rechts) auf, einige auch unter einem Winkel von 40°. Andererseits ist die Rückstrahlung gegen die Bestrahlungsrichtung sehr gering.

Die wichtigste Erkenntnis ist jedoch, dass selbst bei zahlreichen 3D-Auswertungen keine Streuungsmaxima größer als 10^-4 Intensität des bestrahlten Feldes auftraten. Im Falle von Strahlungsleistungen oder Energien muss dieses Verhältnis noch zum Quadrat genommen werden, d.h. die Dichte der gestreuten Leistung ist maximal nur 10^-8 der Dichte der primären bestrahlten Leistung. In der Praxis hat Mie-Streuung nur einen sehr geringen Einfluss auf die Homogenität der primären Strahlung. In Bezug auf die Energie hat der maximale Effekt die 8. Dezimalstelle und ist daher schwer messbar.

Die praktische Bedeutungslosigkeit der Mie-Streuung wird durch die folgenden Fakten und Zusammenhänge bestätigt:

• Das gestreute Feld wurde in einem Abstand von der Streugrenze berechnet, der der Hälfte der Wellenlänge entspricht. Bei größeren Entfernungen nimmt die Intensität des gestreuten Feldes entsprechend ab.
• Dies entspricht der indirekten Streuung auf mehreren Sphären. In diesem Fall werden die Effekte der Kettenstreuung sehr schnell auf extrem kleine Radien verstärkt.
• In einer weiteren Simulation wurde eine relativ einfache komplex bewertete Permittivität mit ionischer Resonanz bei einer Wellenlänge von 10 µm modelliert, wie sie ungefähr bei SiO2 auftritt. Dies zeigte, dass deutliche Minima und Maxima mit der Richtung zu den durchschnittlichen Werten ausgerichtet sind.
• Eine weitere Erhöhung des diffusen Streueffekts wird durch die unregelmäßige Anordnung und Größe der Kugeln in der Farbschicht verursacht, was den maximalen Streueffekt näher an den Mittelwert verschiebt.

Bei der Simulation der Gesamtfeldintensität war klar erkennbar, dass die „Brennpunkte“ bereits innerhalb oder außerhalb der Oberfläche der Kugel gebildet wurden. Insgesamt kann auch gesagt werden, dass Strahlung aus einem großen Bereich fester Winkel auf einen engeren Bereich fester Winkel in Ausbreitungsrichtung konzentriert wird.

Die Simulation der Absorptionseigenschaften erfordert detailliertere Materialdaten, die nur durch Messungen mit vertretbarem Aufwand bestimmt werden können. Im zweiten Fall ist jedoch auch die Simulation veraltet.

Schlussfolgerung: Die Analyse des Problems der Mie-Streuung hat die relevanten Parameter der Mie-Streuung aufgezeigt. Die Mie-Streuung konnte grundsätzlich gut für den Anwendungsbereich modelliert werden und ermöglicht klare Schätzungen der Grenzwerte der Mie-Streuwirkung. Daraus ergibt sich, dass der Mie-Streuungseffekt praktisch keine Bedeutung für die Erklärung der Wirksamkeit des ClimateCoating-Beschichtung hat.

Dies führt zu dem Schluss, dass die Strahlungseigenschaften hauptsächlich durch die Transmission, Absorption und Reflexion an der Farbbeschichtung bestimmt sind. Aufgrund der dünnen Farbschicht durchdringt ein relativ großer Teil der Strahlung die Farbschicht. Der verbleibende Teil könnte durch Absorption und starke Temperaturgradienten an der Oberfläche der Farbe erwärmt werden und als Temperaturstrahler wirken. Dies bestätigt den hohen Wärmewiderstand aufgrund der eingebetteten Hohlräume, den resultierenden verringerten Querschnitt und die längere Bahn in der Acrylmatrize sowie die geringe Wärmekapazität.

Simulácie úspor energie na vykurovanie prostredníctvom použitia technológie termokeramických membrán na vnútorné a/alebo vonkajšie maľovanie budov. (WP 6)

Rechnungsfähiger Schritt: Validierung der Berechnungen und Animationen, Präsentation der Ergebnisse in Woche 14

Basierend auf den Ergebnissen der oben genannten vorläufigen Untersuchungen wurden nun vollständige Simulationen des Raumklimas durchgeführt, die deutlich zeigen, wie die Farbe funktioniert und sie mit der Funktionsweise einer normalen Acrylfarbe vergleichen.

Zu diesem Zweck wurden in zwei Simulationen mit konventioneller Konvektionsheizung und modernem Deckenstrahlheizsystem, wie in Abbildung 15, die linke Seite mit den vollständig beschriebenen physikalischen Effekten mit normaler Acrylfarbe auf der rechten Seite verglichen. Um Überlastungen auf Bodenniveau zu vermeiden, wurde der getestete Körper höher platziert, um einen Luftaustausch in der Nähe des Bodens zu ermöglichen.

Die Temperaturunterschiede rechts und links sind deutlich sichtbar. Darüber hinaus ist eine ruhige Luftzirkulation bei der Strahlungsheizung auf der linken Seite offensichtlich, die nur bei kalten Brücken auf der rechten Seite Turbulenzen aufweist. Im Gegensatz dazu ist bei der Konvektionsheizung die Turbulenz im gesamten Raum relativ hoch.

Vergleich der Temperaturprofile bei zwei Heizsystemen

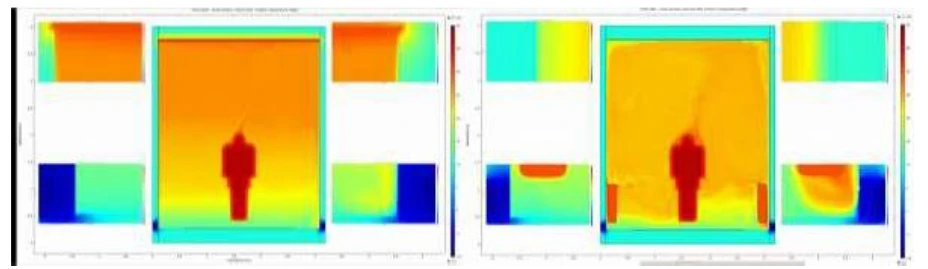
Abbildung 21: Darstellung der Temperaturprofile in einem Testraum mit zwei Heizsystemen und einer Farbbeschichtung: links – ClimateCoating, rechts – Acrylfarbe, wobei beide Farben einen Reflexionsfaktor von 0,5 zugewiesen bekommen haben. Detaillierte Ansichten auf beiden Seiten zeigen die Temperatur der Farbe und die Lufttemperatur in der Grenzschicht. Während die ClimateCoating-Farbe bereits erhitzt ist und die Wandtemperatur sowie die Temperatur der kalten Brücke schützt, hat die Acrylfarbe nach einer Stunde eine deutlich niedrigere Temperatur, ebenso wie die angrenzende Grenzschicht.

Die berechneten Temperaturen sind in Abbildung 21 dargestellt und zeigen erwartete Unterschiede zwischen der rechten und linken Seite im unteren und mittleren Bereich. Auf Kopfhöhe ist der Unterschied gering. Die starken Schwankungen der gemessenen Werte im Fall der Konvektionsheizung sind auf die Luftturbulenzen zurückzuführen.

Körpertemperatur des getesteten Subjekts

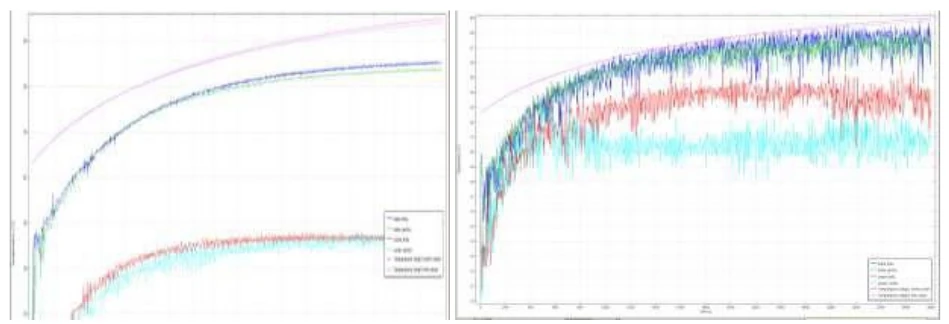
Abbildung 22: Darstellung der Temperaturkurven eines getesteten Subjekts in einem Testraum mit zwei Heizsystemen und einer Farbbeschichtung: links – ClimateCoating, rechts – Acrylfarbe, wobei beiden Farben ein Reflexionsfaktor von 0,5 zugewiesen wurde. In beiden Fällen gibt es einen leichten Unterschied zwischen der rechten und linken Seite, wobei die Konvektionsheizung größere Luftzirkulationen verursacht, was zu größeren Schwankungen der gemessenen Werte führt. Der höhere Strahlungseintrag auf der ClimateCoating-Seite, der durch die Erwärmung der ClimateCoating-Oberfläche resultiert, wird hier nicht angezeigt.

Die Wirkung der Beschichtung lässt sich hervorragend mit diesen Illustrationen erklären. Sie zeigt, wie die linke Seite von ClimateCoating aufgrund ihrer niedrigen Wärmekapazität erhitzt wird, während sie aufgrund der geringen Wärmeleitfähigkeit einen festen Gradienten zur Wand darunter bildet. Die warme Oberfläche wird von den Menschen als angenehm wahrgenommen und trägt eindeutig zu einer guten Atmosphäre bei. Es zeigte sich auch, dass die kalte Brücke nicht auf die Innenfläche eindringen kann. Der Kaltluftstrom wurde nur bis zum unisolierten Boden geleitet. Die Beschichtung kann daher Feuchtigkeit verhindern, die dann an der kalten Oberfläche kondensiert. Dies ist ein weiteres wichtiges Argument für die positive Wirkung der Farbe. Raumheizung mit zwei Heizsystemen.

Verschiedene Farbschichten an den Wänden wurden auch als Video erstellt und dem Unternehmen zur Vorführung auf der Messe zur Verfügung gestellt.

Ein weiterer wichtiger Hinweis zur Wirkung der Beschichtung lässt sich durch die Bestimmung der Energieeinsparung bei der Heizung gewinnen. Zu diesem Zweck wurden zwei Berechnungen mit der Methode der Endgeometrie durchgeführt, mit einem Modell des Raums, das an der linken Wand eine „Außenwand“ und eine Außentemperatur von -10 °C hat. Im Raum war ein Konvektionsheizsystem installiert. Im Inneren wurde ein Konvektionsheizsystem installiert, das je nach Temperatur des Strömungstemperatur (90 °C und 60 °C) unterschiedliche Heizleistungen erzeugte. Jeder dieser beiden Modelle war mit Acrylfarbe oder ClimateCoating-Farbe an der Innenseite und der linken Außenwand gestrichen. Das endgültige Temperaturprofil wurde durch statische Berechnung ermittelt. Die Leistung, die in beiden Fällen durch die Oberfläche des Heizkörpers für fast denselben Endzustand erforderlich war, wurde dann zur Bestimmung der Energieeinsparung beim Heizen dieser beiden Varianten des Raums verwendet.

Variante des Raums mit Acrylfarbe innen und an der linken Außenseite

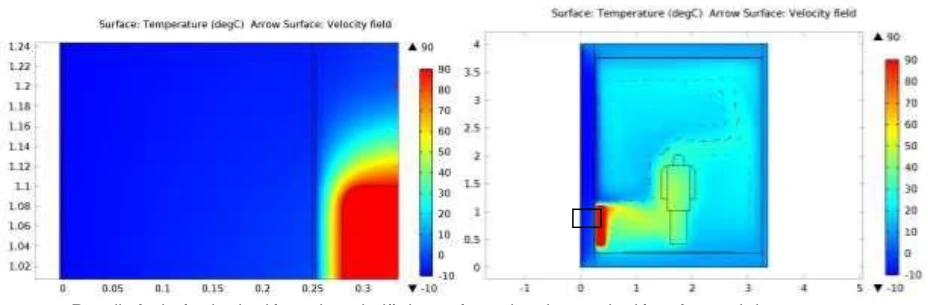
Abb. 23 Darstellung der Temperaturverläufe in einem Testraum mit Konvektionsheizung und einem Farbanstrich bestehend aus Acrylfarbe (Reflexionsfaktor 0,5) an der linken Außenwand und im Inneren. Die Außentemperatur beträgt -10 °C und die Temperatur des Heizkörperdurchflusses beträgt 90 °C. Im Ausschnitt des Bildes, der auf der rechten Seite des Bildes mit einem Rahmen markiert ist, ist eine vollständige Abkühlung der Außenwand und der auf der Oberfläche vorhandene Kaltluftstrom sichtbar. Nur die Luft um die getestete Person hat eine Temperatur von etwa 24/25 °C.

Raumvariante mit ClimateCoating-Beschichtung innen und an der linken Außenseite

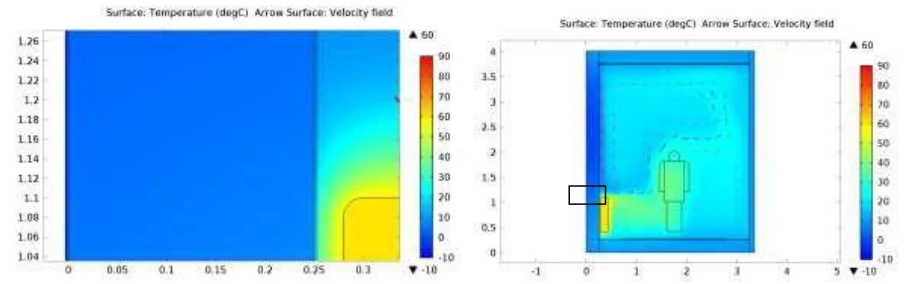
Abb. 24 Darstellung der Temperaturverläufe in einem Testraum mit Konvektionsheizung und einem Farbanstrich bestehend aus ClimateCoating-Farbe (Reflexionsfaktor 0,5) an der linken Außenwand und im Inneren. Die Außentemperatur beträgt -10 °C und die Temperatur des Heizkörperdurchflusses beträgt 60 °C. Im Ausschnitt des Bildes, der auf der rechten Seite des Bildes mit einem Rahmen markiert ist, ist der Temperaturgradient von der äußeren Farbe an der Außenwand zur inneren Farbe sichtbar. Im Inneren gibt es keine Oberfläche mit Kaltluftströmung. Darüber hinaus wird der Raum gleichmäßiger aufgewärmt mit einer Temperatur von etwa 24/25 °C.

Diese beiden Berechnungen lieferten klare Informationen zur Heizleistung. Während im ersten Raum eine Leistung von 108 W/m erforderlich war, um denselben Endzustand zu erreichen, war im zweiten Fall mit ClimateCoating-Beschichtung nur eine Leistung von 63 W/m erforderlich. Dies führt zu einer Energieeinsparung von etwa 40 % bei Verwendung der ClimateCoating-Beschichtung. Das Ergebnis ist eine Energieeinsparung von etwa 40 % bei der Verwendung von ClimateCoating.

Fazit: Durch die Modellierung der Innenmalerei mit ClimateCoating-Beschichtung auf der linken Seite und Acrylbeschichtung auf der rechten Seite konnte eine wichtige Demonstration der Funktionsweise der Beschichtung durchgeführt werden. Es zeigte sich der Isolierungseffekt, die schnelle Erwärmung der Oberfläche und die Auswirkungen der Luftströmung im Vergleich der linken und rechten Seite. Darüber hinaus zeigte sich die Wirkung bei der Kaltbrücke, die normalerweise zu einer feuchten und somit schimmeligen Ecke führt.

Der Effekt der Beschichtung lässt sich hervorragend anhand dieser Illustrationen erklären. Sie zeigt, wie die linke Seite von ClimateCoating aufgrund ihrer niedrigen Wärmekapazität aufgeheizt wird, während durch die geringe Wärmeleitfähigkeit ein starker Gradient zur Wand unter ihr erzeugt wird. Die warme Oberfläche wird von den Menschen als angenehm wahrgenommen und trägt eindeutig zu einer guten Atmosphäre bei. Gleichzeitig zeigte sich, dass die Kältebrücke nicht auf die Innenseite vordringen kann. Der Kaltluftstrom wurde nur in den nicht isolierten Boden geführt. Die Beschichtung kann daher Feuchtigkeit verhindern, die dann auf der kalten Oberfläche kondensiert. Dies ist ein weiteres wichtiges Argument für den positiven Effekt der Farbe. Raumheizung mit zwei Heizsystemen.

Verschiedene Farbschichten an den Wänden wurden auch als Video erstellt und dem Unternehmen zur Vorführung auf der Messe zur Verfügung gestellt.

Ein weiterer wichtiger Hinweis zum Effekt der Beschichtung kann durch die Bestimmung der Heizenergieeinsparung gewonnen werden. Zu diesem Zweck wurden zwei Berechnungen mittels der endgültigen Geometrie-Methode mit einem Raummodell durchgeführt, das eine „Außenwand“ auf der linken Seite und eine Außentemperatur von -10 °C hat. In dem Raum wurde ein konvektives Heizsystem installiert. Im Inneren wurde ein konvektives Heizsystem installiert, das durch unterschiedliche Strömungstemperaturen (90 °C und 60 °C) unterschiedliche Wärmeleistungen erzeugte. Jedes dieser beiden Modelle wurde auf der Innenseite und auf der linken Außenseite mit Acrylfarbe oder ClimateCoating gestrichen. Das endgültige Temperaturprofil wurde durch eine statische Berechnung ermittelt. Die benötigte Leistung in beiden Fällen durch die Radiatoroberfläche für nahezu denselben Endzustand wurde dann verwendet, um die Energieeinsparung für die Heizung dieser beiden Raumvarianten zu berechnen.

Raumvariante mit Acrylfarbe innen und an der linken Außenseite

Abb. 23 Darstellung der Temperaturverläufe im Testraum mit konvektiver Heizung und einer Farbbeschichtung aus Acrylfarbe (Reflexionsfaktor 0,5) an der linken Außenseite und im Innenbereich. Die Außentemperatur beträgt -10 °C und die Temperatur des Radiatorstroms 90 °C. Auf dem Ausschnitt des Bildes, der rechts markiert ist, ist die vollständige Abkühlung der Außenwand und die Oberflächenströmung der kalten Luft zu sehen. Nur die Luft in der Nähe der getesteten Person hat eine Temperatur von etwa 24/25 °C.

Raumvariante mit ClimateCoating-Beschichtung innen und an der linken Außenseite

Abb. 24 Darstellung der Temperaturverläufe im Testraum mit konvektiver Heizung und einer Farbbeschichtung aus ClimateCoating (Reflexionsfaktor 0,5) an der linken Außenseite und im Innenbereich. Die Außentemperatur beträgt -10 °C und die Temperatur des Radiatorstroms 60 °C. Im Abschnitt des Bildes, der rechts markiert ist, ist der Temperaturgradient von der Außenfarbe an der Außenwand und der Innenfarbe zu sehen. Im Inneren gibt es keinen Oberflächenluftstrom der kalten Luft. Darüber hinaus wird der Raum gleichmäßiger mit einer Temperatur von etwa 24/25 °C beheizt.

Diese beiden Berechnungen lieferten eine klare Information über die Heizleistung. Während im ersten Raum eine Leistung von 108 W/m benötigt wurde, um denselben Endzustand zu erreichen, wurde im zweiten Fall mit der ClimateCoating-Beschichtung nur eine Leistung von 63 W/m benötigt. Das Ergebnis ist eine Energieeinsparung von etwa 40 % bei der Verwendung von ClimateCoating. Das Ergebnis ist eine Energieeinsparung von etwa 40 % bei der Verwendung der ClimateCoating-Farbe.

Fazit: Durch die Modellierung der Innenmalerei mit ClimateCoating auf der linken Seite und Acrylfarbe auf der rechten Seite konnte eine wichtige Demonstration der Funktionsweise der Beschichtung durchgeführt werden, wobei der Isolierungseffekt, das schnelle Aufheizen der Oberfläche und der Einfluss des Luftstroms beim Vergleich der linken und rechten Seite gezeigt wurde. Darüber hinaus wurde der Wirkmechanismus im Fall der Kältebrücke gezeigt, die in einem Standardfall zu einem feuchten und damit schimmeligen Eckbereich führt.

About The Author